Local solver for parabolic diffusion equation on hypergraph. More...

#include <advection_parab_ldgh.hxx>

Classes
struct	data_type
	Define type of (hyperedge related) data that is stored in HyDataContainer. More...

struct	error_def
	Define how errors are evaluated. More...

struct	node_element
	Define type of node elements, especially with respect to nodal shape functions. More...

Public Types
typedef std::vector< lSol_float_t >	constructor_value_type
	Class is constructed using a single double indicating the penalty parameter. More...

Public Member Functions
	AdvectionParab (const constructor_value_type &constru=std::vector(3, 1.))
	Constructor for local solver. More...

template<typename hyEdgeT , typename SmallMatInT , typename SmallMatOutT >
SmallMatOutT &	trace_to_flux (const SmallMatInT &lambda_values_in, SmallMatOutT &lambda_values_out, hyEdgeT &hyper_edge, const lSol_float_t time=0.) const
	Evaluate local contribution to matrix–vector multiplication. More...

template<typename hyEdgeT , typename SmallMatInT , typename SmallMatOutT >
SmallMatOutT &	residual_flux (const SmallMatInT &lambda_values_in, SmallMatOutT &lambda_values_out, hyEdgeT &hyper_edge, const lSol_float_t time=0.) const
	Evaluate local contribution to residual. More...

template<class hyEdgeT >
void	set_data (const std::array< std::array< lSol_float_t, n_shape_bdr_ >, 2 *hyEdge_dimT > &lambda_values, hyEdgeT &hyper_edge, const lSol_float_t time=0.) const
	Set data into data container to be used for next time step. More...

template<class hyEdgeT , typename SmallMatT >
SmallMatT &	make_initial (SmallMatT &lambda_values, hyEdgeT &hyper_edge, const lSol_float_t time=0.) const
	L2 project initial data to skeletal and fill data container. More...

template<class hyEdgeT >
std::array< lSol_float_t, 1U >	errors (const std::array< std::array< lSol_float_t, n_shape_bdr_ >, 2 *hyEdge_dimT > &UNUSED(lambda_values), hyEdgeT &hy_edge, const lSol_float_t time=0.) const
	Evaluate squared local L2 error. More...

template<typename abscissa_float_t , std::size_t abscissas_sizeT, class input_array_t , class hyEdgeT >
std::array< std::array< lSol_float_t, Hypercube< hyEdge_dimT >::pow(abscissas_sizeT)>, system_dim >	bulk_values (const std::array< abscissa_float_t, abscissas_sizeT > &abscissas, const input_array_t &, hyEdgeT &hyper_edge, const lSol_float_t UNUSED(time)=0.) const
	Evaluate local local reconstruction at tensorial products of abscissas. More...

Static Public Member Functions
static constexpr unsigned int	hyEdge_dim ()
	Dimension of hyper edge type that this object solves on. More...

static constexpr unsigned int	n_glob_dofs_per_node ()
	Evaluate amount of global degrees of freedom per hypernode. More...

static constexpr unsigned int	system_dimension ()
	Dimension of of the solution evaluated with respect to a hyperedge. More...

static constexpr unsigned int	node_system_dimension ()
	Dimension of of the solution evaluated with respect to a hypernode. More...

Private Types
typedef TPP::Quadrature::Tensorial< TPP::Quadrature::GaussLegendre< quad_deg >, TPP::ShapeFunction< TPP::ShapeType::Tensorial< TPP::ShapeType::Legendre< poly_deg >, hyEdge_dimT > >, lSol_float_t >	integrator
	An integrator helps to easily evaluate integrals (e.g. via quadrature). More...

Private Member Functions
template<typename hyEdgeT >
SmallSquareMat< n_loc_dofs_, lSol_float_t >	assemble_loc_matrix (hyEdgeT &hyper_edge, const lSol_float_t time) const
	Assemble local matrix for the local solver. More...

template<typename hyEdgeT , typename SmallMatT >
SmallVec< n_loc_dofs_, lSol_float_t >	assemble_rhs_from_lambda (const SmallMatT &lambda_values, hyEdgeT &hyper_edge, const lSol_float_t time) const
	Assemble local right-hand for the local solver (from skeletal). More...

template<typename hyEdgeT >
SmallVec< n_loc_dofs_, lSol_float_t >	assemble_rhs_from_global_rhs (hyEdgeT &hyper_edge, const lSol_float_t time) const
	Assemble local right-hand for the local solver (from global right-hand side). More...

template<typename hyEdgeT , typename SmallMatT >
std::array< lSol_float_t, n_loc_dofs_ >	solve_local_problem (const SmallMatT &lambda_values, const unsigned int solution_type, hyEdgeT &hyper_edge, const lSol_float_t time) const
	Solve local problem (with right-hand side from skeletal). More...

template<typename SmallMatT , typename hyEdgeT >
std::array< std::array< lSol_float_t, n_shape_bdr_ >, 2 *hyEdge_dimT >	flux_at_boundary (const SmallMatT &lambda_values, const std::array< lSol_float_t, n_loc_dofs_ > &coeffs, hyEdgeT &hyper_edge, const bool residual, const lSol_float_t time) const
	Evaluate flux at boundary. More...

Static Private Member Functions
template<typename parameters , typename hyEdge_t >
static constexpr bool	is_dirichlet (const hyEdge_t &edge, const unsigned int face, const lSol_float_t time)
	Find out whether a node is of Dirichlet type. More...

template<typename parameters , typename hyEdge_t >
static constexpr bool	is_outflow (const hyEdge_t &edge, const unsigned int face, const lSol_float_t time)

Private Attributes
const lSol_float_t	tau_
	(Globally constant) penalty parameter for HDG scheme. More...

const lSol_float_t	theta_
	Parameter theta that defines the one-step theta scheme. More...

const lSol_float_t	delta_t_
	Time step size. More...

Static Private Attributes
static constexpr unsigned int	n_shape_fct_ = n_glob_dofs_per_node() * (poly_deg + 1)
	Number of local shape functions (with respect to all spatial dimensions). More...

static constexpr unsigned int	n_shape_bdr_ = n_glob_dofs_per_node()
	Number oflocal shape functions (with respect to a face / hypernode). More...

static constexpr unsigned int	n_loc_dofs_ = n_shape_fct_
	Number of (local) degrees of freedom per hyperedge. More...

static constexpr unsigned int	system_dim = system_dimension()
	Dimension of of the solution evaluated with respect to a hypernode. More...

static constexpr unsigned int	node_system_dim = node_system_dimension()
	Dimension of of the solution evaluated with respect to a hypernode. More...

Detailed Description

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>
class LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >

Local solver for parabolic diffusion equation on hypergraph.

Note: Theta must be one, since only implicit Euler has been implemented at the moment.

This class contains the local solver for an isotropic diffusion equation, i.e.,

\[ \partial_t u - \nabla \cdot ( d \nabla u ) = f \quad \text{ in } \Omega, \qquad u = u_\text D \quad \text{ on } \partial \Omega_\text D, \qquad - d \nabla u \cdot \nu = g_\text N \quad \text{ on } \partial \Omega_\text N \]

in a spatial domain \(\Omega \subset \mathbb R^d\). Here, \(d\) is the spatial dimension space_dim, \(\Omega\) is a regular graph (hyEdge_dimT = 1) or hypergraph whose hyperedges are surfaces (hyEdge_dimT = 2) or volumes (hyEdge_dimT = 3) or hypervolumes (in case of hyEdge_dimT > 3). \(f\) and \(d\) are scalars defined in the whole domain, the Dirichlet and Neumann boundary data needs to be defined on their respective hypernodes.

Template Parameters

hyEdge_dimT	Dimension of a hyperedge, i.e., 1 is for PDEs defined on graphs, 2 is for PDEs defined on surfaces, and 3 is for PDEs defined on volumes.
poly_deg	The polynomial degree of test and trial functions.
quad_deg	The order of the quadrature rule.
parametersT	Struct depending on templates `space_dimTP` and `lSol_float_TP` that contains static parameter functions. Defaults to above functions included in `DiffusionParametersDefault`.
lSol_float_t	The floating point type calculations are executed in. Defaults to double.

Authors: Guido Kanschat, Heidelberg University, 2019–2020.; Andreas Rupp, Heidelberg University, 2019–2020.

Member Typedef Documentation

◆ constructor_value_type

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

typedef std::vector<lSol_float_t> LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::constructor_value_type

Class is constructed using a single double indicating the penalty parameter.

◆ integrator

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

typedef TPP::Quadrature::Tensorial< TPP::Quadrature::GaussLegendre<quad_deg>, TPP::ShapeFunction<TPP::ShapeType::Tensorial<TPP::ShapeType::Legendre<poly_deg>, hyEdge_dimT> >, lSol_float_t> LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::integrator

private

An integrator helps to easily evaluate integrals (e.g. via quadrature).

Constructor & Destructor Documentation

◆ AdvectionParab()

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::AdvectionParab ( const constructor_value_type & constru = std::vector(3, 1.) )

inline

Constructor for local solver.

Parameters

constru Constructor object.

Member Function Documentation

◆ assemble_loc_matrix()

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

template<typename hyEdgeT >

SmallSquareMat<n_loc_dofs_, lSol_float_t> LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::assemble_loc_matrix	(	hyEdgeT &	hyper_edge,
		const lSol_float_t	time
	)		const

inlineprivate

Assemble local matrix for the local solver.

Template Parameters

hyEdgeT The geometry type / typename of the considered hyEdge's geometry.

Parameters

hyper_edge	The geometry of the considered hyperedge (of typename GeomT).
time	Time, when the local matrix is evaluated.

Return values

loc_mat Matrix of the local solver.

◆ assemble_rhs_from_global_rhs()

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

template<typename hyEdgeT >

SmallVec<n_loc_dofs_, lSol_float_t> LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::assemble_rhs_from_global_rhs	(	hyEdgeT &	hyper_edge,
		const lSol_float_t	time
	)		const

inlineprivate

Assemble local right-hand for the local solver (from global right-hand side).

Note that we basically follow the lines of

B. Cockburn, J. Gopalakrishnan, and R. Lazarov. Unified hybridization of discontinuous Galerkin, mixed, and continuous Galerkin methods for second order elliptic problems. SIAM Journal on Numerical Analysis, 47(2):1319–1365, 2009

and discriminate between local solvers with respect to the skeletal variable and with respect to the global right-hand side. This assembles the local right-hand side with respect to the global right-hand side. This function implicitly uses the parameters.

Template Parameters

hyEdgeT The geometry type / typename of the considered hyEdge's geometry.

Parameters

hyper_edge	The geometry of the considered hyperedge (of typename GeomT).
time	Point of time, rhs is evaluated at

Return values

loc_rhs Local right hand side of the locasl solver.

◆ assemble_rhs_from_lambda()

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

template<typename hyEdgeT , typename SmallMatT >

SmallVec<n_loc_dofs_, lSol_float_t> LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::assemble_rhs_from_lambda	(	const SmallMatT &	lambda_values,
		hyEdgeT &	hyper_edge,
		const lSol_float_t	time
	)		const

inlineprivate

Assemble local right-hand for the local solver (from skeletal).

The right hand side needs the values of the global degrees of freedom. Note that we basically follow the lines of

B. Cockburn, J. Gopalakrishnan, and R. Lazarov. Unified hybridization of discontinuous Galerkin, mixed, and continuous Galerkin methods for second order elliptic problems. SIAM Journal on Numerical Analysis, 47(2):1319–1365, 2009

and discriminate between local solvers with respect to the skeletal variable and with respect to the global right-hand side. This assembles the local right-hand side with respect to the skeletal variable.

Template Parameters

hyEdgeT	The geometry type / typename of the considered hyEdge's geometry.
SmallMatT	The data type of the \¢ lambda_values.

Parameters

lambda_values	Global degrees of freedom associated to the hyperedge.
hyper_edge	The geometry of the considered hyperedge (of typename GeomT).
time	The time at which functions are evbaluated.

Return values

loc_rhs Local right hand side of the locasl solver.

◆ bulk_values()

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

template<typename abscissa_float_t , std::size_t abscissas_sizeT, class input_array_t , class hyEdgeT >

std::array<std::array<lSol_float_t, Hypercube<hyEdge_dimT>::pow(abscissas_sizeT)>, system_dim> LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::bulk_values	(	const std::array< abscissa_float_t, abscissas_sizeT > &	abscissas,
		const input_array_t &	,
		hyEdgeT &	hyper_edge,
		const lSol_float_t	UNUSEDtime = `0.`
	)		const

Evaluate local local reconstruction at tensorial products of abscissas.

Template Parameters

abscissa_float_t	Floating type for the abscissa values.
abscissas_sizeT	Size of the array of array of abscissas.
input_array_t	Input array type.
hyEdgeT	The geometry type / typename of the considered hyEdge's geometry.

Parameters

abscissas	Abscissas of the supporting points.
hyper_edge	The geometry of the considered hyperedge (of typename GeomT).
time	Time at which function is plotted.

Return values

func_vals Array of function values.

◆ errors()

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

template<class hyEdgeT >

std::array<lSol_float_t, 1U> LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::errors	(	const std::array< std::array< lSol_float_t, n_shape_bdr_ >, 2 *hyEdge_dimT > &	UNUSEDlambda_values,
		hyEdgeT &	hy_edge,
		const lSol_float_t	time = `0.`
	)		const

inline

Evaluate squared local L2 error.

Template Parameters

hyEdgeT The geometry type / typename of the considered hyEdge's geometry.

Parameters

lambda_values	The values of the skeletal variable's coefficients.
hy_edge	The geometry of the considered hyperedge (of typename GeomT).
time	Time at which error is evaluated.

Return values

err	Local squared L2 error.

◆ flux_at_boundary()

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

template<typename SmallMatT , typename hyEdgeT >

std::array<std::array<lSol_float_t, n_shape_bdr_>, 2 * hyEdge_dimT> LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::flux_at_boundary	(	const SmallMatT &	lambda_values,
		const std::array< lSol_float_t, n_loc_dofs_ > &	coeffs,
		hyEdgeT &	hyper_edge,
		const bool	residual,
		const lSol_float_t	time
	)		const

inlineprivate

Evaluate flux at boundary.

Template Parameters

SmallMatT	The tyoe of lambda_values.
hyEdgeT	The geometry type / typename of the considered hyEdge's geometry.

Parameters

lambda_values	Coefficients of skeletal variable.
coeffs	Coefficients of the local solution.
hyper_edge	The geometry of the considered hyperedge (of typename GeomT).
residual	Boolean to discriminate betweeen lambda_to_flux and residual_flux.
time	Time at which functions are evaluated.

Return values

bdr_coeffs Coefficients of respective (dim-1) dimensional function at boundaries.

◆ hyEdge_dim()

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

static constexpr unsigned int LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::hyEdge_dim ( )

inlinestaticconstexpr

Dimension of hyper edge type that this object solves on.

◆ is_dirichlet()

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

template<typename parameters , typename hyEdge_t >

static constexpr bool LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::is_dirichlet	(	const hyEdge_t &	edge,
		const unsigned int	face,
		const lSol_float_t	time
	)

inlinestaticconstexprprivate

Find out whether a node is of Dirichlet type.

Here is the call graph for this function:

◆ is_outflow()

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

template<typename parameters , typename hyEdge_t >

static constexpr bool LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::is_outflow	(	const hyEdge_t &	edge,
		const unsigned int	face,
		const lSol_float_t	time
	)

inlinestaticconstexprprivate

Here is the call graph for this function:

◆ make_initial()

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

template<class hyEdgeT , typename SmallMatT >

SmallMatT& LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::make_initial	(	SmallMatT &	lambda_values,
		hyEdgeT &	hyper_edge,
		const lSol_float_t	time = `0.`
	)		const

inline

L2 project initial data to skeletal and fill data container.

Template Parameters

hyEdgeT	The geometry type / typename of the considered hyEdge's geometry.
SmallMatT	The data tyepe of `lambda_values`.

Parameters

lambda_values	Local part of vector x.
hyper_edge	The geometry of the considered hyperedge (of typename GeomT).
time	Initial time of parabolic problem.

Return values

vecAx L2 projected initial datum.

Here is the call graph for this function:

◆ n_glob_dofs_per_node()

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

static constexpr unsigned int LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::n_glob_dofs_per_node ( )

inlinestaticconstexpr

Evaluate amount of global degrees of freedom per hypernode.

This number must be equal to HyperNodeFactory::n_dofs_per_node() of the HyperNodeFactory cooperating with this object.

Return values

n_dofs Number of global degrees of freedom per hypernode.

Here is the call graph for this function:

◆ node_system_dimension()

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

static constexpr unsigned int LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::node_system_dimension ( )

inlinestaticconstexpr

Dimension of of the solution evaluated with respect to a hypernode.

◆ residual_flux()

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

template<typename hyEdgeT , typename SmallMatInT , typename SmallMatOutT >

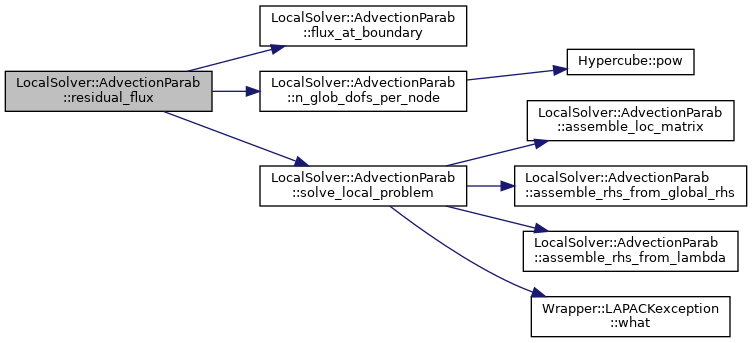
SmallMatOutT& LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::residual_flux	(	const SmallMatInT &	lambda_values_in,
		SmallMatOutT &	lambda_values_out,
		hyEdgeT &	hyper_edge,
		const lSol_float_t	time = `0.`
	)		const

inline

Evaluate local contribution to residual.

Execute residual evaluation y = A * x - b, where x represents the vector containing the skeletal variable (adjacent to one hyperedge), and A is the condensed matrix arising from the HDG discretization. This function does this multiplication (locally) for one hyperedge. The hyperedge is no parameter, since all hyperedges are assumed to have the same properties.

Template Parameters

hyEdgeT	The geometry type / typename of the considered hyEdge's geometry.
SmallMatInT	Data type of `lambda_values_in`.
SmallMatOutT	Data type of `lambda_values_out`.

Parameters

lambda_values_in	Local part of vector x.
lambda_values_out	Local part that will be added to A * x.
hyper_edge	The geometry of the considered hyperedge (of typename GeomT).
time	Time at which time step ends.

Return values

vecAx Local part of vector A * x.

Here is the call graph for this function:

◆ set_data()

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

template<class hyEdgeT >

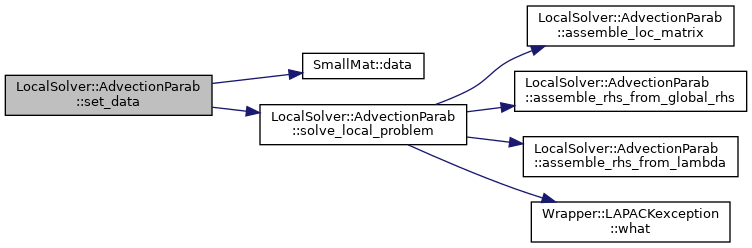
void LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::set_data	(	const std::array< std::array< lSol_float_t, n_shape_bdr_ >, 2 *hyEdge_dimT > &	lambda_values,
		hyEdgeT &	hyper_edge,
		const lSol_float_t	time = `0.`
	)		const

inline

Set data into data container to be used for next time step.

Template Parameters

hyEdgeT The geometry type / typename of the considered hyEdge's geometry.

Parameters

lambda_values	Local part of vector x.
hyper_edge	The geometry of the considered hyperedge (of typename GeomT).
time	Time at which the old time step ended.

Here is the call graph for this function:

◆ solve_local_problem()

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

template<typename hyEdgeT , typename SmallMatT >

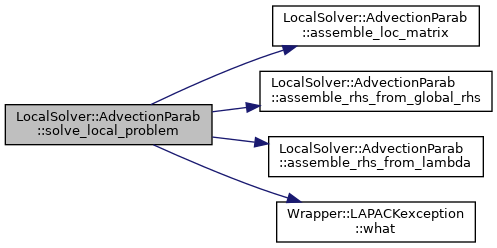
std::array<lSol_float_t, n_loc_dofs_> LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::solve_local_problem	(	const SmallMatT &	lambda_values,
		const unsigned int	solution_type,
		hyEdgeT &	hyper_edge,
		const lSol_float_t	time
	)		const

inlineprivate

Solve local problem (with right-hand side from skeletal).

Template Parameters

hyEdgeT	The geometry type / typename of the considered hyEdge's geometry.
SmallMatT	The data type of the `lambda_values`.

Parameters

lambda_values	Global degrees of freedom associated to the hyperedge.
solution_type	Type of local problem that is to be solved.
hyper_edge	The geometry of the considered hyperedge (of typename GeomT).
time	Point of time the problem is solved.

Return values

loc_sol Solution of the local problem.

Here is the call graph for this function:

◆ system_dimension()

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

static constexpr unsigned int LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::system_dimension ( )

inlinestaticconstexpr

Dimension of of the solution evaluated with respect to a hyperedge.

◆ trace_to_flux()

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

template<typename hyEdgeT , typename SmallMatInT , typename SmallMatOutT >

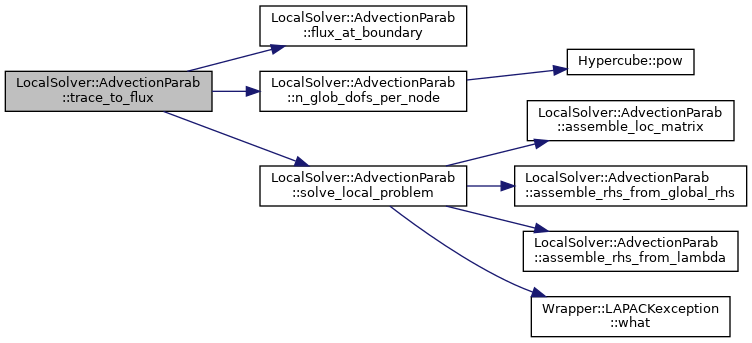
SmallMatOutT& LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::trace_to_flux	(	const SmallMatInT &	lambda_values_in,
		SmallMatOutT &	lambda_values_out,
		hyEdgeT &	hyper_edge,
		const lSol_float_t	time = `0.`
	)		const

inline

Evaluate local contribution to matrix–vector multiplication.

Execute matrix–vector multiplication y = A * x, where x represents the vector containing the skeletal variable (adjacent to one hyperedge), and A is the condensed matrix arising from the HDG discretization. This function does this multiplication (locally) for one hyperedge. The hyperedge is no parameter, since all hyperedges are assumed to have the same properties.

Template Parameters

hyEdgeT	The geometry type / typename of the considered hyEdge's geometry.
SmallMatInT	Data type of `lambda_values_in`.
SmallMatOutT	Data type of `lambda_values_out`

Parameters

lambda_values_in	Local part of vector x.
lambda_values_out	Local part that will be added to A * x.
hyper_edge	The geometry of the considered hyperedge (of typename GeomT).
time	Time at which time step ends.

Return values

vecAx Local part of vector A * x.

Here is the call graph for this function:

Member Data Documentation

◆ delta_t_

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

const lSol_float_t LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::delta_t_

private

Time step size.

◆ n_loc_dofs_

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

constexpr unsigned int LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::n_loc_dofs_ = n_shape_fct_

staticconstexprprivate

Number of (local) degrees of freedom per hyperedge.

◆ n_shape_bdr_

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

constexpr unsigned int LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::n_shape_bdr_ = n_glob_dofs_per_node()

staticconstexprprivate

Number oflocal shape functions (with respect to a face / hypernode).

◆ n_shape_fct_

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

constexpr unsigned int LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::n_shape_fct_ = n_glob_dofs_per_node() * (poly_deg + 1)

staticconstexprprivate

Number of local shape functions (with respect to all spatial dimensions).

◆ node_system_dim

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

constexpr unsigned int LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::node_system_dim = node_system_dimension()

staticconstexprprivate

Dimension of of the solution evaluated with respect to a hypernode.

This allows to the use of this quantity as template parameter in member functions.

◆ system_dim

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

constexpr unsigned int LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::system_dim = system_dimension()

staticconstexprprivate

Dimension of of the solution evaluated with respect to a hypernode.

This allows to the use of this quantity as template parameter in member functions.

◆ tau_

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

const lSol_float_t LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::tau_

private

(Globally constant) penalty parameter for HDG scheme.

◆ theta_

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>

const lSol_float_t LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >::theta_

private

Parameter theta that defines the one-step theta scheme.

The documentation for this class was generated from the following file:

/home/runner/work/HyperHDG/HyperHDG/include/HyperHDG/local_solver/advection_parab_ldgh.hxx

Classes

Public Types

Public Member Functions

Static Public Member Functions

Private Types

Private Member Functions

Static Private Member Functions

Private Attributes

Static Private Attributes

Detailed Description

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double> class LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >

Member Typedef Documentation

◆ constructor_value_type

◆ integrator

Constructor & Destructor Documentation

◆ AdvectionParab()

Member Function Documentation

◆ assemble_loc_matrix()

◆ assemble_rhs_from_global_rhs()

◆ assemble_rhs_from_lambda()

◆ bulk_values()

◆ errors()

◆ flux_at_boundary()

◆ hyEdge_dim()

◆ is_dirichlet()

◆ is_outflow()

◆ make_initial()

◆ n_glob_dofs_per_node()

◆ node_system_dimension()

◆ residual_flux()

◆ set_data()

◆ solve_local_problem()

◆ system_dimension()

◆ trace_to_flux()

Member Data Documentation

◆ delta_t_

◆ n_loc_dofs_

◆ n_shape_bdr_

◆ n_shape_fct_

◆ node_system_dim

◆ system_dim

◆ tau_

◆ theta_

template<unsigned int hyEdge_dimT, unsigned int poly_deg, unsigned int quad_deg, template< unsigned int, typename > typename parametersT = DiffusionParametersDefault, typename lSol_float_t = double>
class LocalSolver::AdvectionParab< hyEdge_dimT, poly_deg, quad_deg, parametersT, lSol_float_t >