A namespace containing different functions that implement basic linear algebra operations using large vectors. More...
Classes | |
| struct | SolveException |
| Exception to be thrown if conjugate gradient fails. More... | |
Functions | |
| template<typename vectorT > | |
| vectorT::value_type | inner_product (const vectorT &left, const vectorT &right) |
| Evaluate the inner product of two vectors. More... | |
| template<typename vectorT > | |
| vectorT::value_type | norm_2 (const vectorT &vec) |
| Evaluate 2 norm of a vector. More... | |
| template<typename vectorT > | |
| vectorT | linear_combination (const typename vectorT::value_type leftFac, const vectorT &leftVec, const typename vectorT::value_type rightFac, const vectorT &rightVec) |
| Evaluate linear combination of vectors and return the result. More... | |
| template<typename vectorT > | |
| void | linear_combination (const typename vectorT::value_type leftFac, const vectorT &leftV, const typename vectorT::value_type rightFac, const vectorT &rightV, vectorT &result) |
| Evaluate linear combination of vectors and return reference to result. More... | |
| template<class ProblemT , typename vectorT > | |
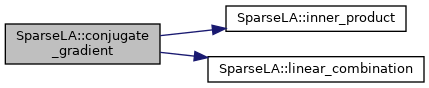
| vectorT | conjugate_gradient (const vectorT &b, ProblemT &problem, unsigned int n_iterations=0, const typename vectorT::value_type tolerance=1e-9) |
| Execute conjugate gradient algorithm to find solution to system of equations. More... | |
Detailed Description
A namespace containing different functions that implement basic linear algebra operations using large vectors.
This namespace provides several functions to implement basic linear algebra operations of (long) vector type in combination with a class providing a function matrix_vector_multiply. This is mainly used for C++ examples and test cases that do not use the Python interface and its version of an CG method, for example.
Function Documentation
◆ conjugate_gradient()
| vectorT SparseLA::conjugate_gradient | ( | const vectorT & | b, |
| ProblemT & | problem, | ||
| unsigned int | n_iterations = 0, |
||
| const typename vectorT::value_type | tolerance = 1e-9 |
||
| ) |
Execute conjugate gradient algorithm to find solution to system of equations.
Execute conjugate gradient algorithm where the matrix is not explicitly given, but the template class ProblemT is supposed to implement a function matrix_vector_multiply which only takes a large vector and generates the matrix vector product from that. The associated matrix is assumed to be square and symmetric positive definite.
- Template Parameters
-
ProblemT Class to implement matrix vector multiplication. vectorT The class name of the large vector.
- Parameters
-
b Right-hand side of linear system of equations. problem Class instantiation to implement matrix vector multiplication. n_iterations Maximum number of iterations. 0 is default and the size of b. tolerance Absolute tolerance value in 2 norm. Default is 1e-9.
- Return values
-
solution Vector sufficing Ax = b up to given tolerance if converged. n_iterations Number of needed iterations. -1 indicates no convergence.
◆ inner_product()
| vectorT::value_type SparseLA::inner_product | ( | const vectorT & | left, |
| const vectorT & | right | ||
| ) |
Evaluate the inner product of two vectors.
Naive implementation of an Euclidean inner product of two large vectors which are supposed to be of the same size. This function is needed to calculate a vector's 2 norm or to implement a CG scheme.
- Template Parameters
-
vectorT The class name of the large vector.
- Parameters
-
left Left argument of the inner product. right Right argument of the inner product.
- Return values
-
product Inner product of the two arguments.
◆ linear_combination() [1/2]
| void SparseLA::linear_combination | ( | const typename vectorT::value_type | leftFac, |
| const vectorT & | leftV, | ||
| const typename vectorT::value_type | rightFac, | ||
| const vectorT & | rightV, | ||
| vectorT & | result | ||
| ) |
Evaluate linear combination of vectors and return reference to result.
This functions takes two large vectors and two floating points, and returns their linear combination "leftFac * leftVec + rightFac * rightVec" as a reference to a vector. This vector needs to be passed to the function
- Template Parameters
-
vectorT The class name of the large vector.
- Parameters
-
leftFac Scaling factor of left vector. leftV Left vector in linear combination. rightFac Scaling factor of right vector. rightV Right vector in linear combination. result Reference to vector whicb is supposed to contain the result.
- Return values
-
result Linear combination of vectors with respective coefficients.
◆ linear_combination() [2/2]
| vectorT SparseLA::linear_combination | ( | const typename vectorT::value_type | leftFac, |
| const vectorT & | leftVec, | ||
| const typename vectorT::value_type | rightFac, | ||
| const vectorT & | rightVec | ||
| ) |
Evaluate linear combination of vectors and return the result.
This functions takes two large vectors and two floating points, and returns their linear combination "leftFac * leftVec + rightFac * rightVec" as a new vector (in contrast to just a reference to a vector).
- Template Parameters
-
vectorT The class name of the large vector.
- Parameters
-
leftFac Scaling factor of left vector. leftVec Left vector in linear combination. rightFac Scaling factor of right vector. rightVec Right vector in linear combination.
- Return values
-
lin_comb Linear combination of vectors with respective coefficients.
◆ norm_2()
| vectorT::value_type SparseLA::norm_2 | ( | const vectorT & | vec | ) |
Evaluate 2 norm of a vector.
Naive implementation of an 2 norm of a vector. This is the square root of the inner_product of a vector paired with itself.
- Template Parameters
-
vectorT The class name of the large vector.
- Parameters
-
vec Vector whose 2 norm is to be calculates.
- Return values
-
norm 2 norm of given vector.

 1.8.17
1.8.17